Le centre de gravité, ou centre de gravité, est le point d'un triangle de la masse de l'équilibre. Pour aider à visualiser cela, imaginez que vous avez une mosaïque triangulaire suspendue au-dessus de la pointe d'un crayon. La vignette en équilibre si la pointe du crayon est placé en son centre de gravité. Trouver le centre de gravité peut être nécessaire dans diverses conception et l'ingénierie, et peut être trouvé en utilisant une géométrie simple.
Mesures
@@_
@@
Méthode 1
à l'Aide d'Intersection des Médianes

1
@@_
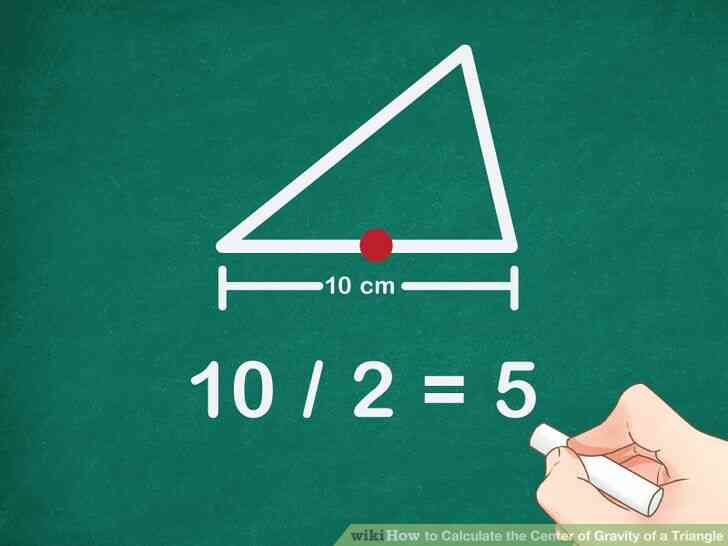
@@Trouver le milieu d'un côté du triangle. Afin de trouver le milieu, de mesurer le côté, et de diviser la longueur de la moitié. L'étiquette du milieu A.
- Par exemple, si un côté du triangle est de 10 cm de long, le milieu sera à 5 cm, depuis 10/2=5{\displaystyle 10/2=5}.
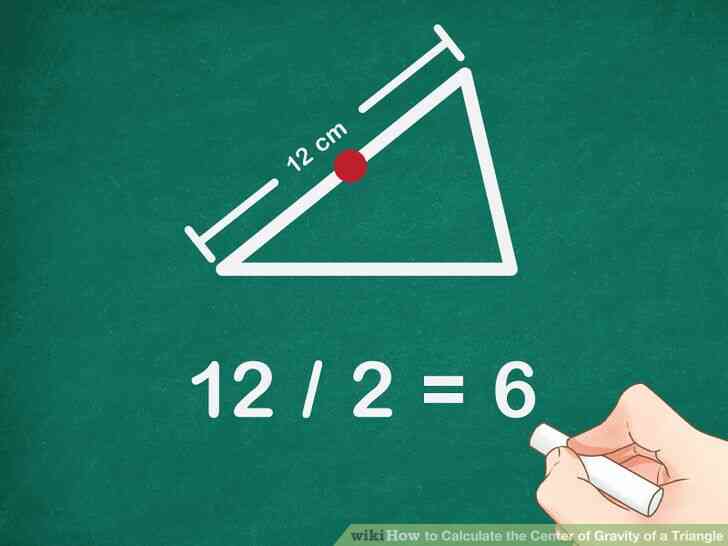
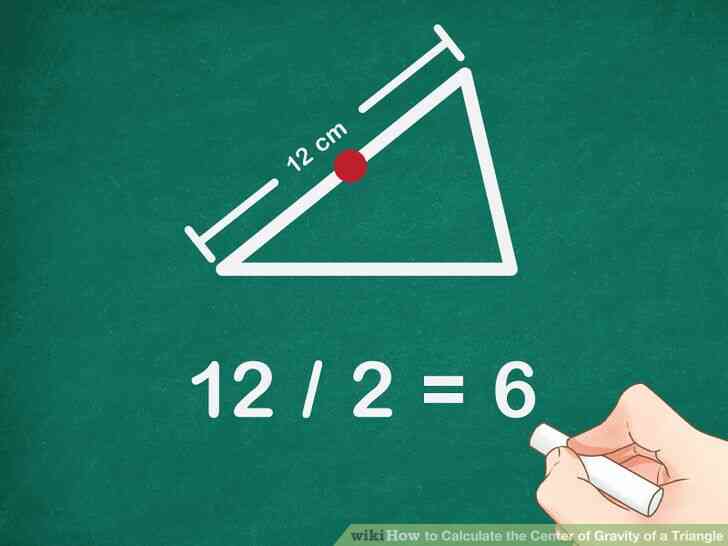
2
@@_
@@Trouver le milieu d'un deuxième côté du triangle. Mesurer la longueur de la côte, et de diviser la longueur de la moitié. L'étiquette du milieu B.
- Par exemple, si le côté du triangle est de 12 cm de long, le milieu sera à 6 cm, depuis 12/2=6{\displaystyle 12/2=6}.

3
@@_
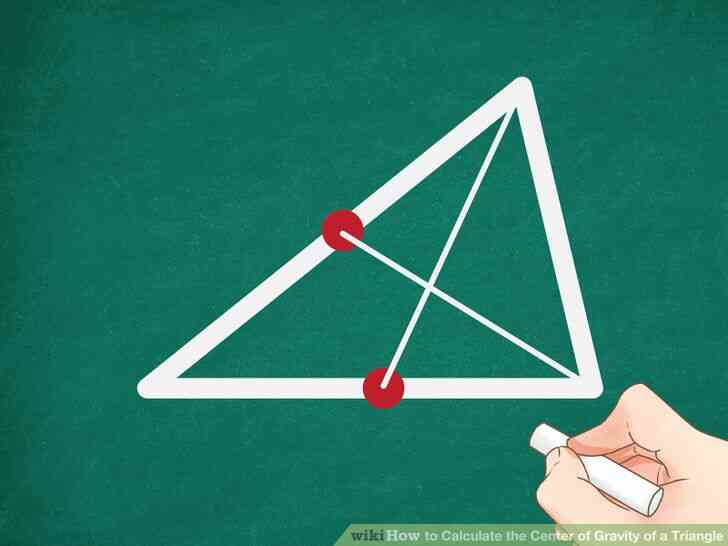
@@Tracez une ligne à partir du milieu de chaque côté de son sommet opposé. Ces deux lignes sont les médianes de chaque côté. [1]
- Un sommet est le point où les deux côtés d'un triangle de répondre.

4
@@_
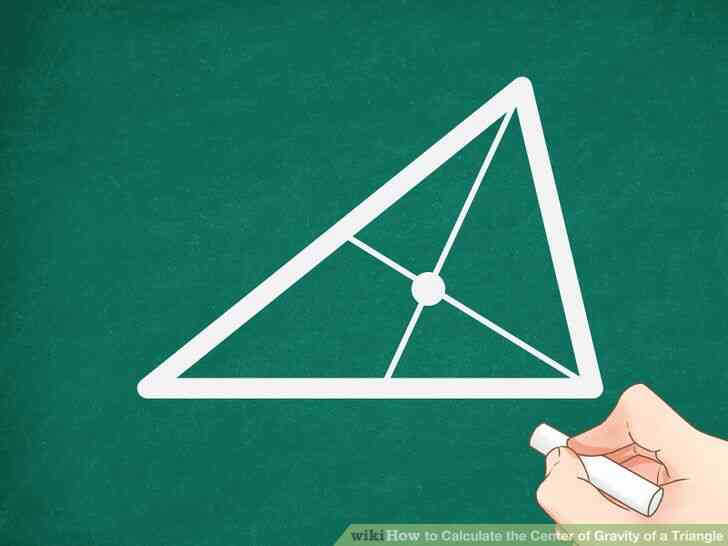
@@Dessiner un point où les deux médianes se coupent. Ce point est le triangle de centre de gravité, aussi appelé le centre de gravité, ou centre de masse. [2][3]
- Le centre de gravité est l'endroit où les trois médianes se coupent, mais depuis les médianes seulement se coupent en un même point, vous pouvez utiliser un raccourci et trouver le centre de gravité par la seule recherche de l'intersection de deux médianes.
@@_
@@
Méthode 2
en Utilisant le Ratio de 2:1

1
@@_
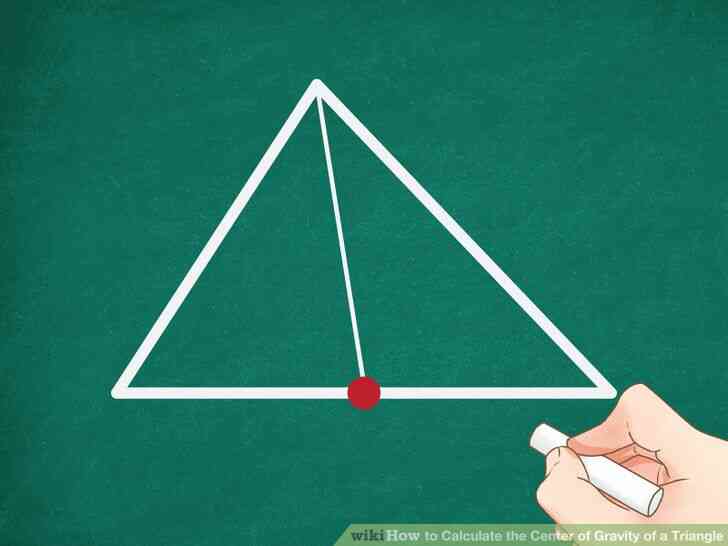
@@Tracer une médiane de votre triangle. Rappelez-vous, la médiane est d'une ligne tracée à partir du milieu d'un côté pour le sommet opposé. Vous pouvez utiliser n'importe quel médiane dans le triangle.

2
@@_
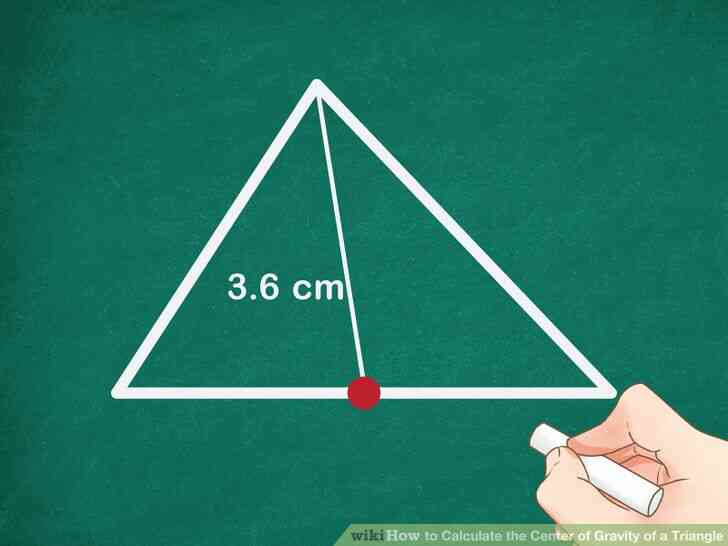
@@Mesurer la longueur de la médiane. Assurez-vous que la mesure est exacte.
- Par exemple, vous pourriez avoir une médiane qui est de 3.6 cm de long.


3
@@_
@@Diviser la longueur de la médiane en tiers. Pour ce faire, divisez la longueur par trois. Encore une fois, faire un calcul exact. Si autour de vous, vous ne trouverez pas le centre de gravité.
- Par exemple, si votre revenu médian est de 3.6 cm de long, vous diviserez 3.6 par 3:3,6 cm/3=1.2 cm{\displaystyle 3,6 cm/3=1.2 cm}, donc ? de la médiane est de 1,2 cm.

4
@@_
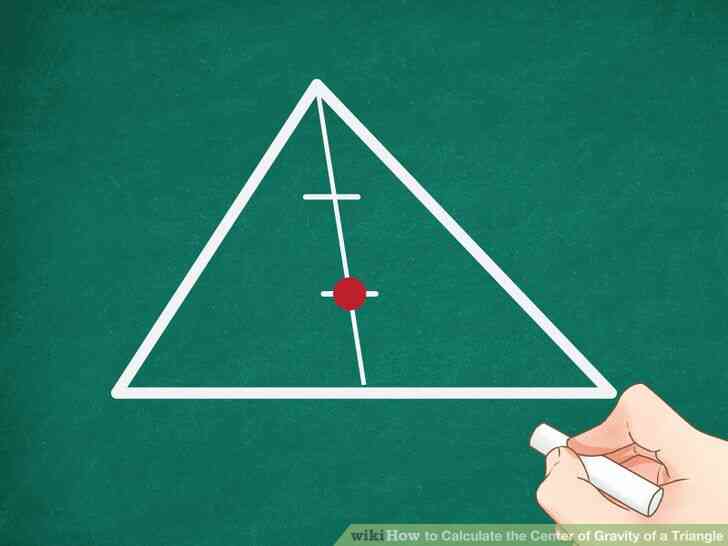
@@Marquer un point sur la médiane ? à partir du milieu. Ce point est le centre de gravité du triangle, qui sera toujours diviser une médiane dans un ratio de 2:1, qui est le centre de gravité est ? la médiane de la distance entre le point milieu et ? la médiane de la distance à partir du sommet.[4]
- Par exemple, sur une ligne médiane est de 3.6 cm de long, le centre de gravité sera de 1,2 cm à partir du milieu.
@@_
@@
Méthode 3
à l'Aide de la Moyenne des Coordonnées

1
@@_
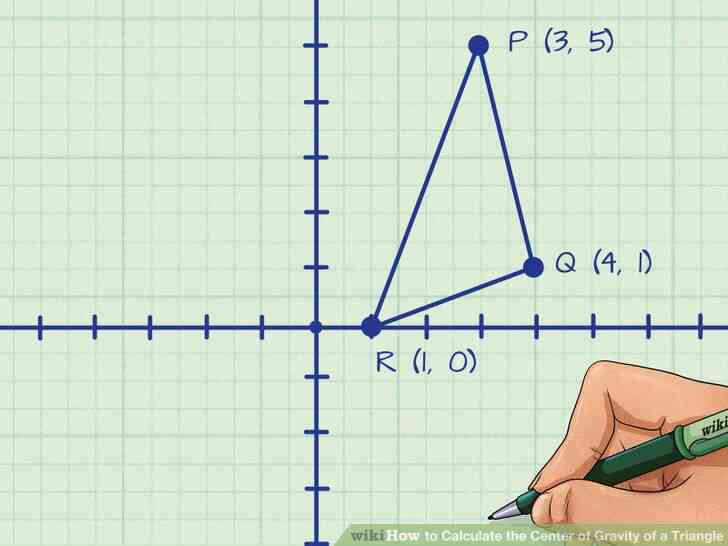
@@Déterminer les coordonnées des trois sommets du triangle. Cette méthode ne fonctionne que si vous travaillez avec un système de coordonnées planes. Coordonnées peut-être déjà donné, ou vous pouvez avoir un triangle dessiné sur un graphe sans les coordonnées étiquetés. Rappelez-vous que les coordonnées doivent être répertoriés (x,y){\displaystyle (x,y)}.
- Par exemple, vous pourriez être donné triangle PQR, et vous avez besoin de trouver et d'étiquette de point P (3, 5), point Q (4, 1) et R (1, 0).
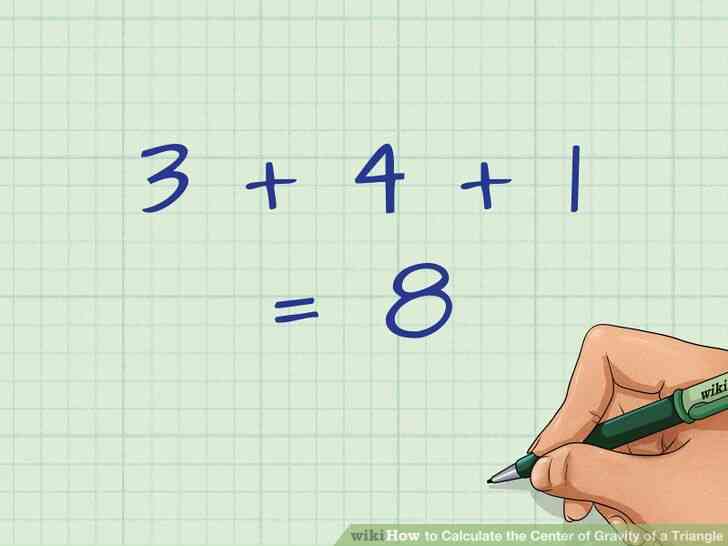
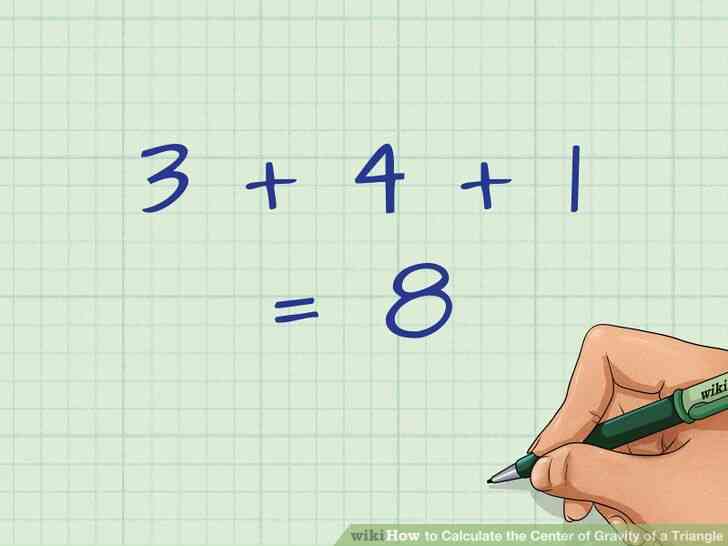
2
@@_
@@Ajoutez la valeur des abscisses. N'oubliez pas d'ajouter tous les trois coordonnées. Vous n'aurez pas calculer le bon centre de gravité si vous n'utilisez que deux coordonnées.
- Par exemple, si vos trois coordonnées x sont 3, 4, et 1, ajouter ces trois valeurs: 3 4 1=8{\displaystyle 3 4 1=8}.
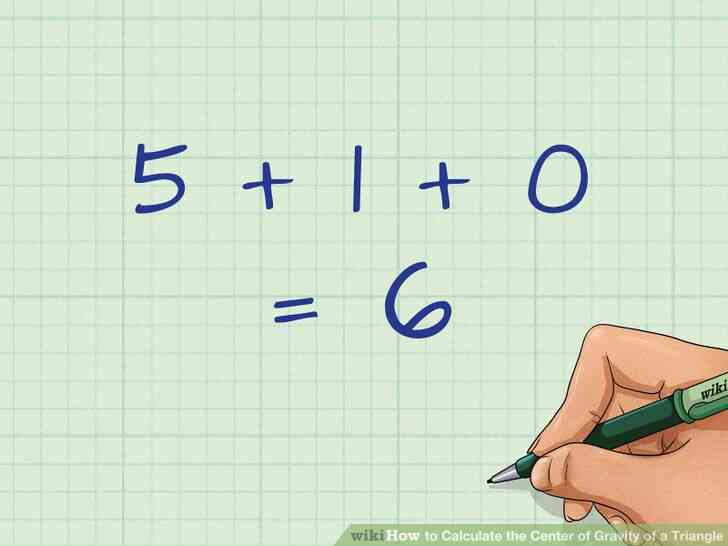
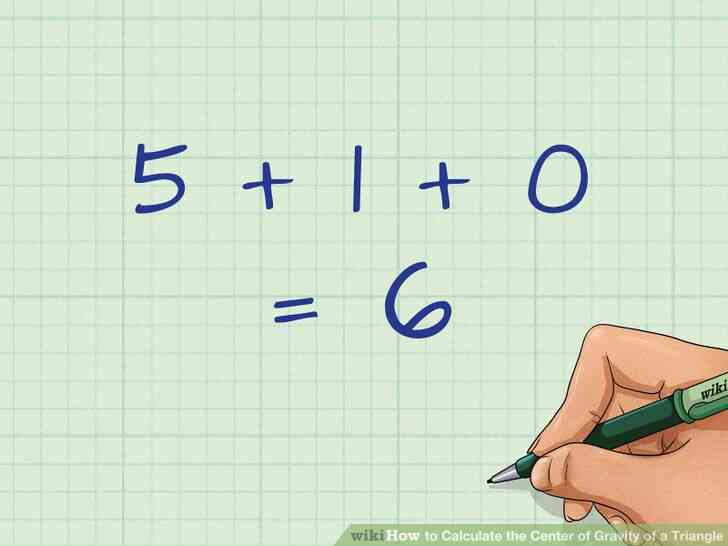
3
@@_
@@Ajoutez la valeur de l'axe des coordonnées. N'oubliez pas d'ajouter tous les trois coordonnées.
- Par exemple, si vos trois coordonnées y sont de 5, 1, et 0, ajouter ces trois valeurs: 5 1 0=6{\displaystyle 5 1 0=6}.
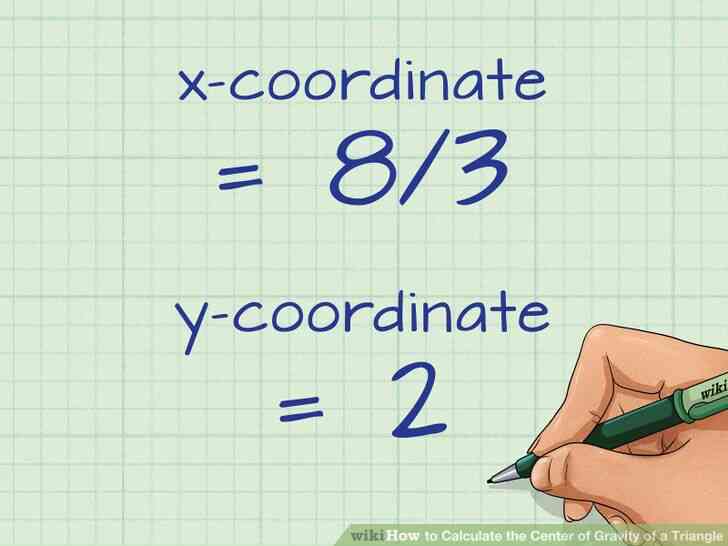
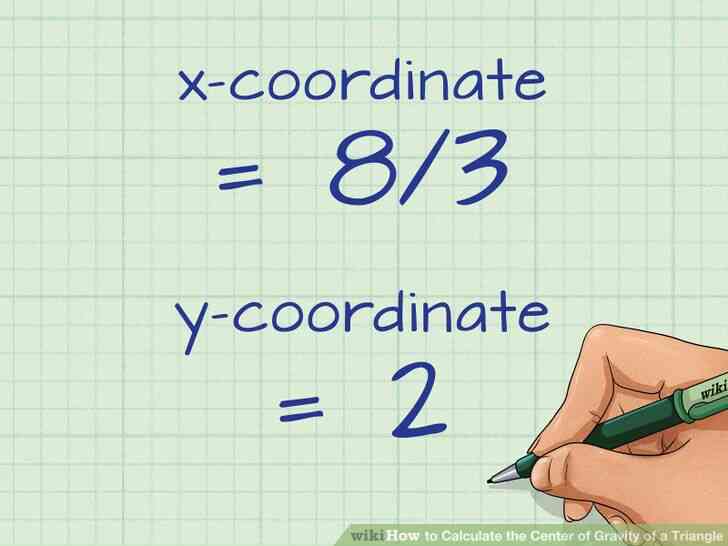
4
@@_
@@Trouver la moyenne de x et y des coordonnées. Ces coordonnées correspondent à la triangle de centre de gravité, aussi connu comme le centre de gravité ou le centre de masse.[5] Pour trouver la moyenne, divisez la somme des coordonnées par 3.
- Par exemple, si la somme de vos coordonnées x est 8, la moyenne de la coordonnée x est 8/3{\displaystyle 8/3}. Si la somme de vos coordonnées y est de 6, la moyenne de la coordonnée y est 6/3{\displaystyle 6/3} 2{\displaystyle 2}.

5
@@_
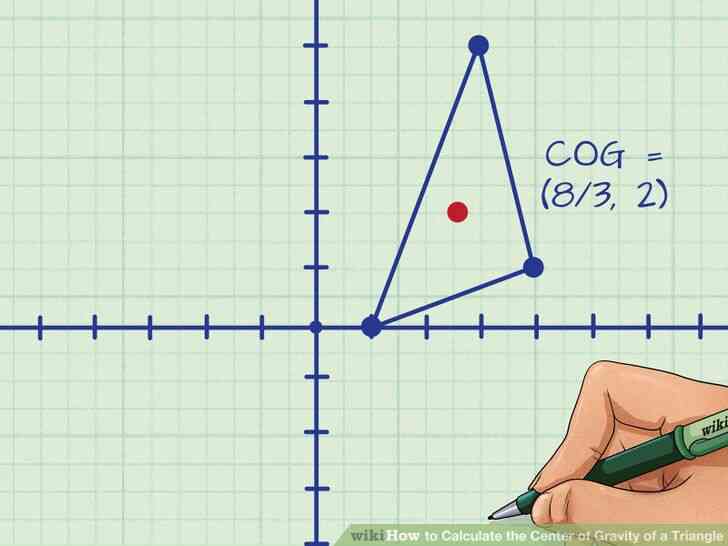
@@Tracer le centre de gravité du triangle. Le centre de gravité, ou centre de gravité, est la moyenne des x et y des coordonnées.
- Dans l'exemple du problème, le centre de gravité est le point (8/3,2){\displaystyle (8/3,2)}.
Comment Calculer le Centre de Gravite d'un Triangle
Le centre de gravite, ou centre de gravite, est le point d'un triangle de la masse de l'equilibre. Pour aider a visualiser cela, imaginez que vous avez une mosaïque triangulaire suspendue au-dessus de la pointe d'un crayon. La vignette en equilibre si la pointe du crayon est place en son centre de gravite. Trouver le centre de gravite peut etre necessaire dans diverses conception et l'ingenierie, et peut etre trouve en utilisant une geometrie simple.
Mesures
@@_
@@
Methode 1
a l'Aide d'Intersection des Medianes


1
@@_
@@Trouver le milieu d'un cote du triangle. Afin de trouver le milieu, de mesurer le cote, et de diviser la longueur de la moitie. L'etiquette du milieu A.
- Par exemple, si un cote du triangle est de 10 cm de long, le milieu sera a 5 cm, depuis 10/2=5{\displaystyle 10/2=5}.
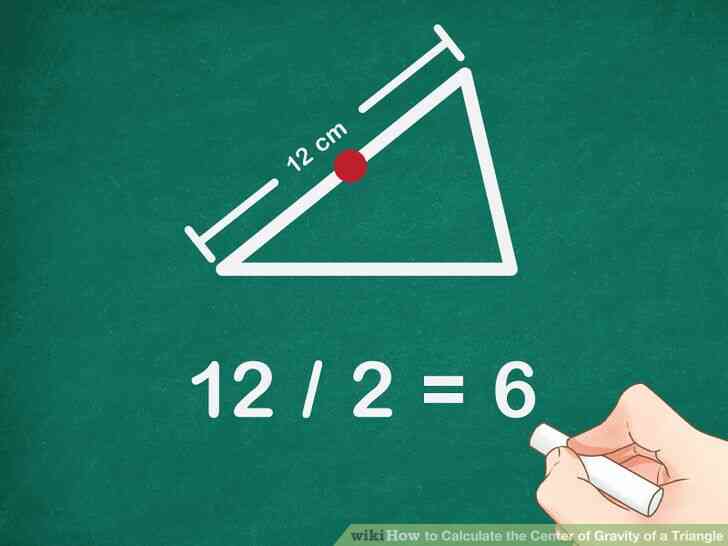
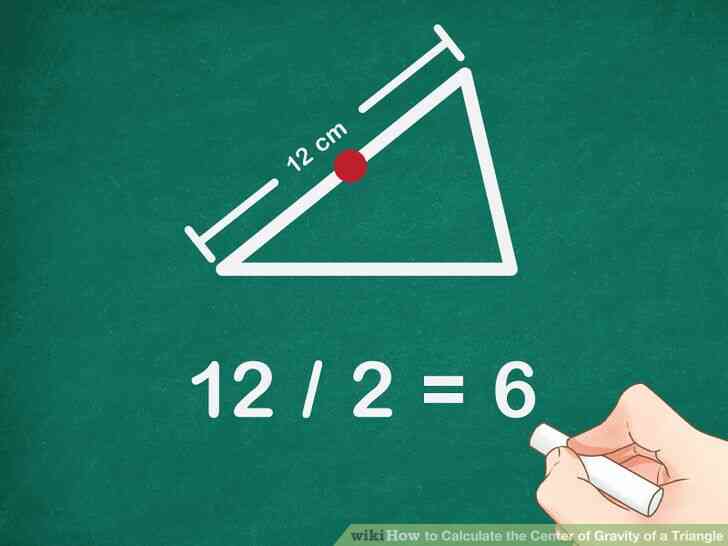
2
@@_
@@Trouver le milieu d'un deuxieme cote du triangle. Mesurer la longueur de la cote, et de diviser la longueur de la moitie. L'etiquette du milieu B.
- Par exemple, si le cote du triangle est de 12 cm de long, le milieu sera a 6 cm, depuis 12/2=6{\displaystyle 12/2=6}.


3
@@_
@@Tracez une ligne a partir du milieu de chaque cote de son sommet oppose. Ces deux lignes sont les medianes de chaque cote. [1]
- Un sommet est le point ou les deux cotes d'un triangle de repondre.


4
@@_
@@Dessiner un point ou les deux medianes se coupent. Ce point est le triangle de centre de gravite, aussi appele le centre de gravite, ou centre de masse. [2][3]
- Le centre de gravite est l'endroit ou les trois medianes se coupent, mais depuis les medianes seulement se coupent en un meme point, vous pouvez utiliser un raccourci et trouver le centre de gravite par la seule recherche de l'intersection de deux medianes.
@@_
@@
Methode 2
en Utilisant le Ratio de 2:1


1
@@_
@@Tracer une mediane de votre triangle. Rappelez-vous, la mediane est d'une ligne tracee a partir du milieu d'un cote pour le sommet oppose. Vous pouvez utiliser n'importe quel mediane dans le triangle.


2
@@_
@@Mesurer la longueur de la mediane. Assurez-vous que la mesure est exacte.
- Par exemple, vous pourriez avoir une mediane qui est de 3.6 cm de long.


3
@@_
@@Diviser la longueur de la mediane en tiers. Pour ce faire, divisez la longueur par trois. Encore une fois, faire un calcul exact. Si autour de vous, vous ne trouverez pas le centre de gravite.
- Par exemple, si votre revenu median est de 3.6 cm de long, vous diviserez 3.6 par 3:3,6 cm/3=1.2 cm{\displaystyle 3,6 cm/3=1.2 cm}, donc ? de la mediane est de 1,2 cm.


4
@@_
@@Marquer un point sur la mediane ? a partir du milieu. Ce point est le centre de gravite du triangle, qui sera toujours diviser une mediane dans un ratio de 2:1, qui est le centre de gravite est ? la mediane de la distance entre le point milieu et ? la mediane de la distance a partir du sommet.[4]
- Par exemple, sur une ligne mediane est de 3.6 cm de long, le centre de gravite sera de 1,2 cm a partir du milieu.
@@_
@@
Methode 3
a l'Aide de la Moyenne des Coordonnees


1
@@_
@@Determiner les coordonnees des trois sommets du triangle. Cette methode ne fonctionne que si vous travaillez avec un systeme de coordonnees planes. Coordonnees peut-etre deja donne, ou vous pouvez avoir un triangle dessine sur un graphe sans les coordonnees etiquetes. Rappelez-vous que les coordonnees doivent etre repertories (x,y){\displaystyle (x,y)}.
- Par exemple, vous pourriez etre donne triangle PQR, et vous avez besoin de trouver et d'etiquette de point P (3, 5), point Q (4, 1) et R (1, 0).
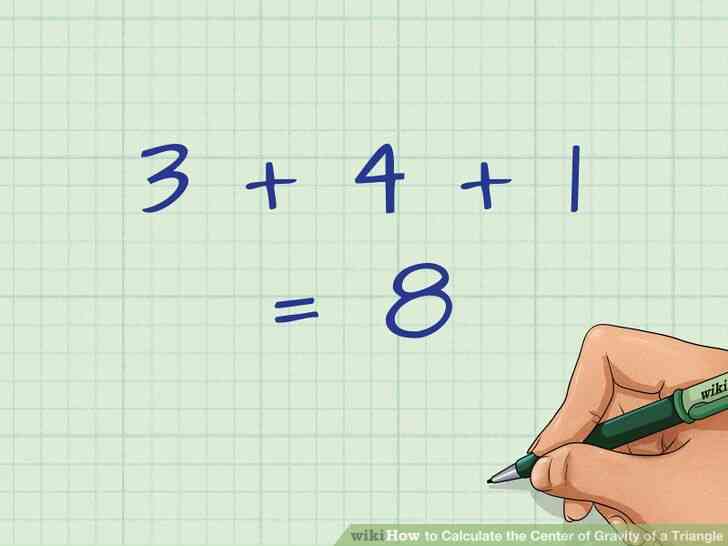
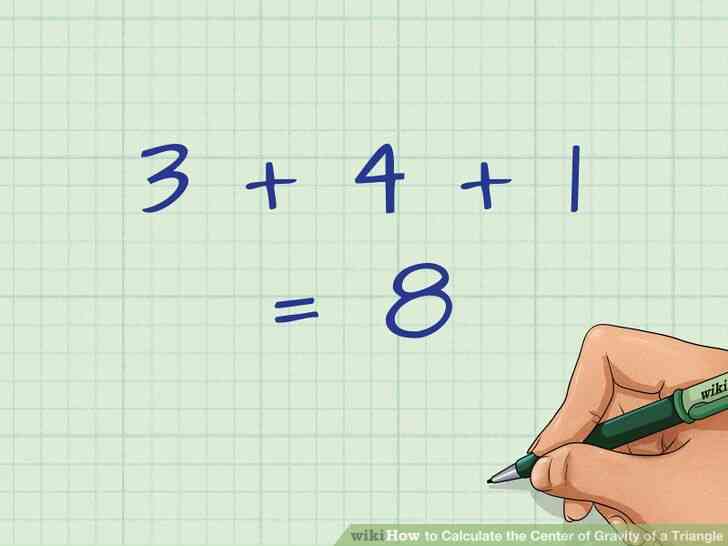
2
@@_
@@Ajoutez la valeur des abscisses. N'oubliez pas d'ajouter tous les trois coordonnees. Vous n'aurez pas calculer le bon centre de gravite si vous n'utilisez que deux coordonnees.
- Par exemple, si vos trois coordonnees x sont 3, 4, et 1, ajouter ces trois valeurs: 3 4 1=8{\displaystyle 3 4 1=8}.
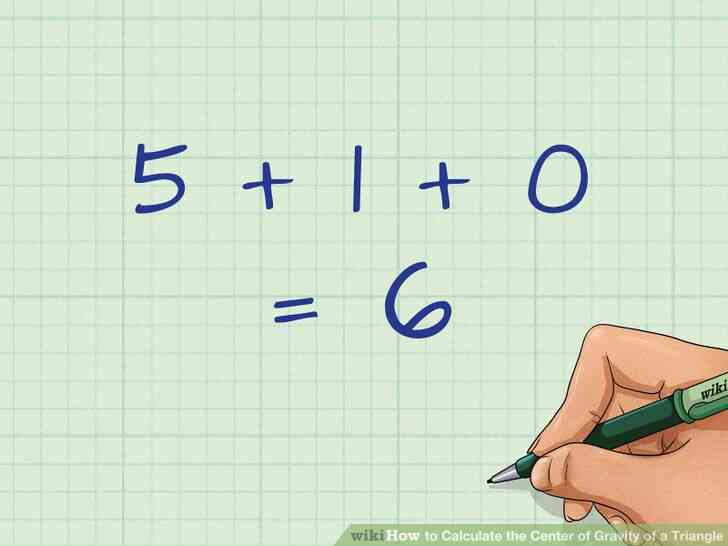
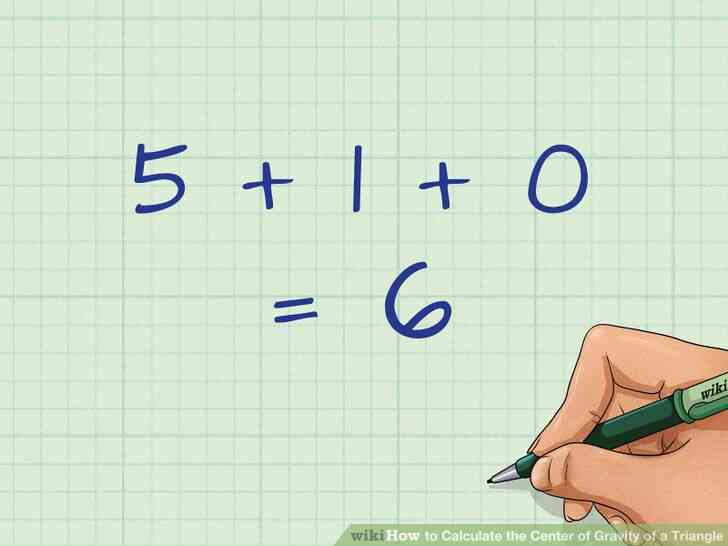
3
@@_
@@Ajoutez la valeur de l'axe des coordonnees. N'oubliez pas d'ajouter tous les trois coordonnees.
- Par exemple, si vos trois coordonnees y sont de 5, 1, et 0, ajouter ces trois valeurs: 5 1 0=6{\displaystyle 5 1 0=6}.
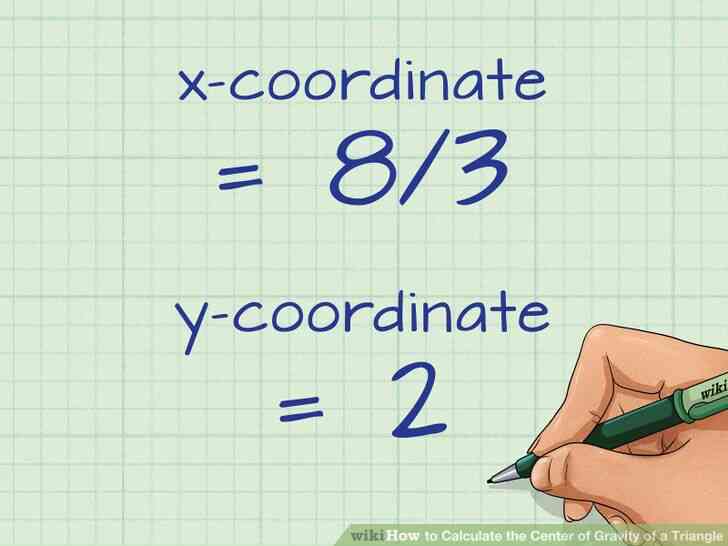
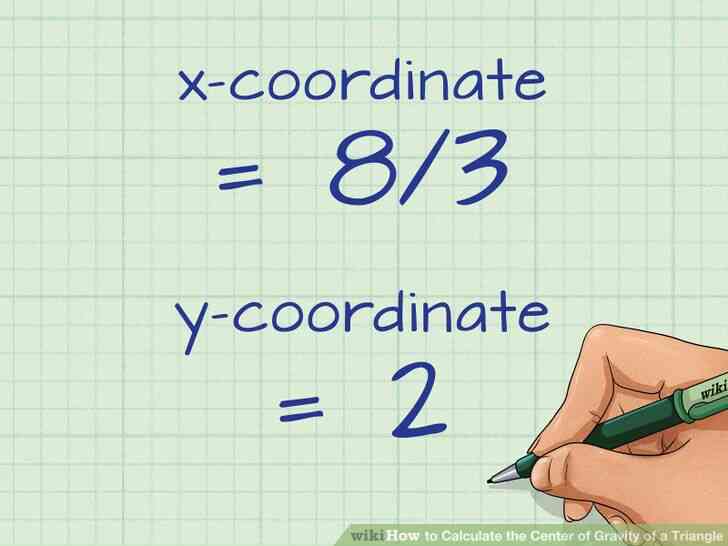
4
@@_
@@Trouver la moyenne de x et y des coordonnees. Ces coordonnees correspondent a la triangle de centre de gravite, aussi connu comme le centre de gravite ou le centre de masse.[5] Pour trouver la moyenne, divisez la somme des coordonnees par 3.
- Par exemple, si la somme de vos coordonnees x est 8, la moyenne de la coordonnee x est 8/3{\displaystyle 8/3}. Si la somme de vos coordonnees y est de 6, la moyenne de la coordonnee y est 6/3{\displaystyle 6/3} 2{\displaystyle 2}.


5
@@_
@@Tracer le centre de gravite du triangle. Le centre de gravite, ou centre de gravite, est la moyenne des x et y des coordonnees.
- Dans l'exemple du probleme, le centre de gravite est le point (8/3,2){\displaystyle (8/3,2)}.
Comment Calculer le Centre de Gravité d'un Triangle
By commentfaire
Le centre de gravité, ou centre de gravité, est le point d'un triangle de la masse de l'équilibre. Pour aider à visualiser cela, imaginez que vous avez une mosaïque triangulaire suspendue au-dessus de la pointe d'un crayon. La vignette en équilibre si la pointe du crayon est placé en son centre de gravité. Trouver le centre de gravité peut être nécessaire dans diverses conception et l'ingénierie, et peut être trouvé en utilisant une géométrie simple.