Vous pouvez déterminer si une fonction est pair, impair, ou ni en regardant l'équation elle-même ou en regardant un graphique de cette fonction. À la fois la méthode algébrique et le graphique de la méthode sont assez simple, mais c'est une bonne idée de les mettre en pratique à la fois, de sorte que vous pouvez répondre à la question quel que soit le type d'information que vous avez sur la main.
Mesures
@@_
@@
Méthode 1
à l'Aide de l'Algèbre
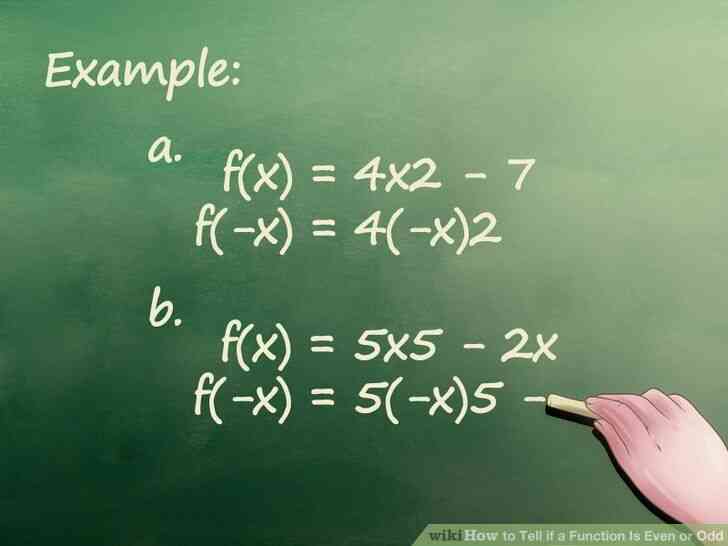
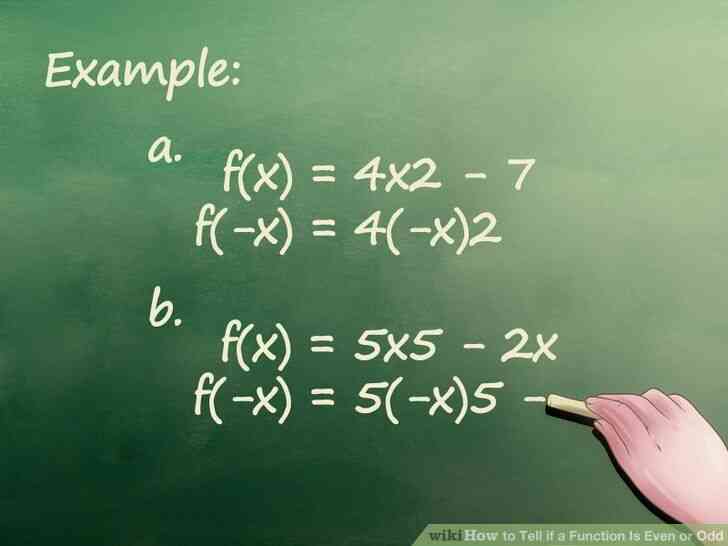
1
@@_
@@Plug-x dans la fonction d'origine. Regardez la fonction d'origine et de localiser la variable x. Chaque fois que vous voyez un x dans la fonction, remplacer-x.[1]
- Un Exemple: f(x) = 4x2 - 7
- dans l'Exemple B: f(x) = 5x5 - 2x
- Exemple C: f(x) = 7x2 5x 3
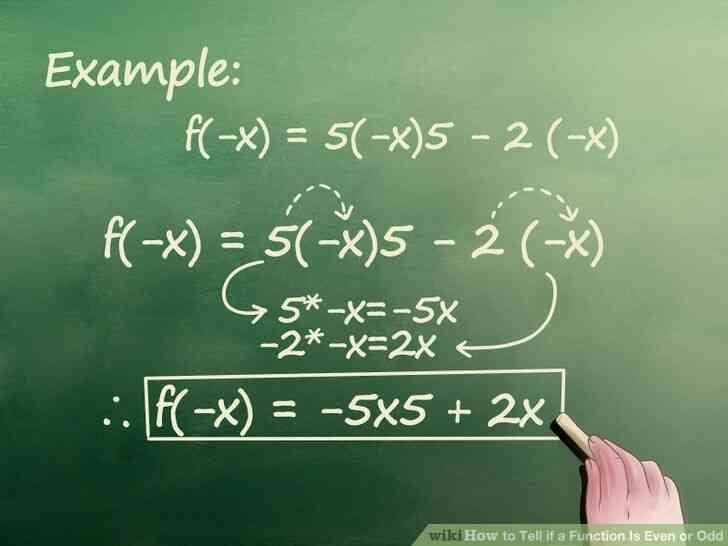
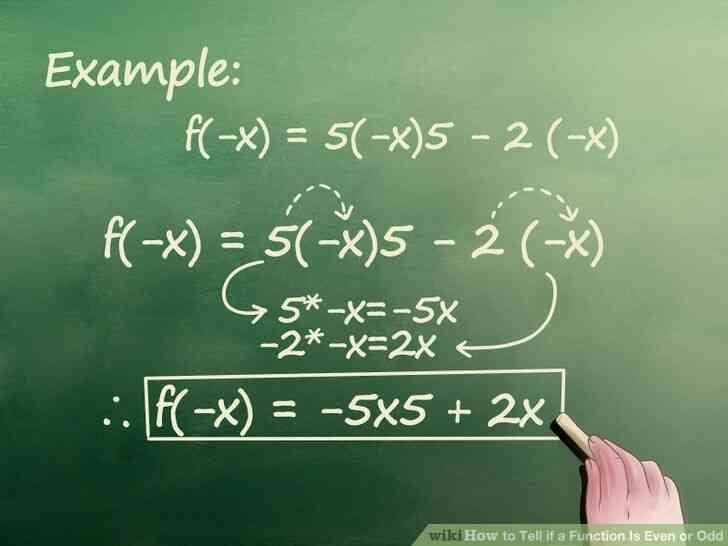
2
@@_
@@Résoudre l'équation. Évaluer l'équation en appliquant vos connaissances des exposants et la multiplication de se débarrasser de l'inutile, les signes négatifs.
- Un Exemple: f(-x) = 4(-x)2 - 7
- Un exposant négatif multiplié par lui-même un même nombre de fois va avoir un effet positif. C'est le principe mathématique que deux négatifs de l'égalité positive en termes de multiplication.
- f(-x) = 4(x)2 - 7
- dans l'Exemple B: f(-x) = 5(-x)5 - 2 (-x)
- Un exposant négatif multiplié par lui-même un nombre impair de fois donne un résultat négatif. En outre, un signe négatif devant un exposant devra être multipliée par le signe plus ou moins, qui se présente devant elle, et un signe négatif multiplié par un signe de la soustraction résultat sera un signe plus.
- f(-x) = -5 x 5 2x
- Exemple C: f(-x) = 7(-x)2 5(-x) 3
- Encore une fois, regardez les exposants, ainsi que les signes plus et moins. Même les exposants auront pour résultat une valeur positive de x et de l'impair exposants un résultat négatif, x. Un signe négatif multiplié par un signe plus permettra de transformer le plus dans un signe moins, et vice-versa.
- f(-x) = 7x2 - 5x 3


3
@@_
@@Analyser les résultats. Si votre fonction est la même que celle de votre départ de la fonction, la fonction est la même. Si le résultat est à l'opposé ou négative de votre départ de la fonction, la fonction est impaire. Si elle n'est pas vraie, la fonction est ni le même ni impair.[2]
- Dans une même fonction, à la fois le début et la fin des fonctions doit être exactement le même.
- Dans une fonction bizarre, tous les signes plus ( + ) doit devenir un signe moins et tous les signes moins doivent devenir des signes plus.
- Lorsqu'il est écrit en symboles algébriques:
- Pour une même fonction: f(x) = f(-x)
- Pour une fonction bizarre: f(-x) = -f(x)
- ni: f(-x) ? f(x) f(-x) ? -f(x)
- Un Exemple: f(x) = 4x2 - 7
- f(-x) = 4(x)2 - 7
- Cette fonction est la même.
- Remarque, également, que chaque x dans une même fonction ont généralement un exposant positif.
- dans l'Exemple B: f(x) = 5 x 5 - 2x
- f(-x) = -5 x 5 2x
- Cette fonction est impaire.
- de manière générale, chaque partie de la fonction aura besoin d'être accompagné par un x avec un étrange exposant de la fonction elle-même étrange.
- Exemple C: f(x) = 7x2 5x 3
- f(-x) = 7x2 - 5x 3
- Cette fonction est ni le même ni impair.
- Lorsque pairs et impairs, les exposants sont mélangés à l'intérieur d'une fonction, cette fonction sera probablement ni même ni impair.
@@_
@@
Méthode 2
à l'Aide de Graphiques
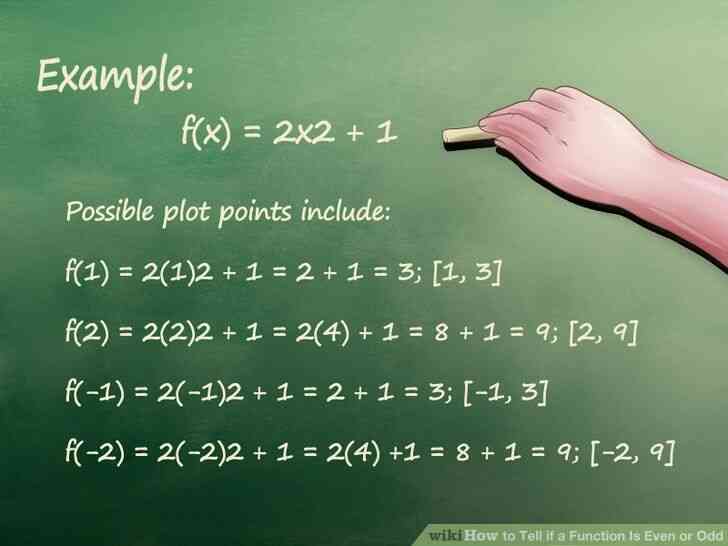
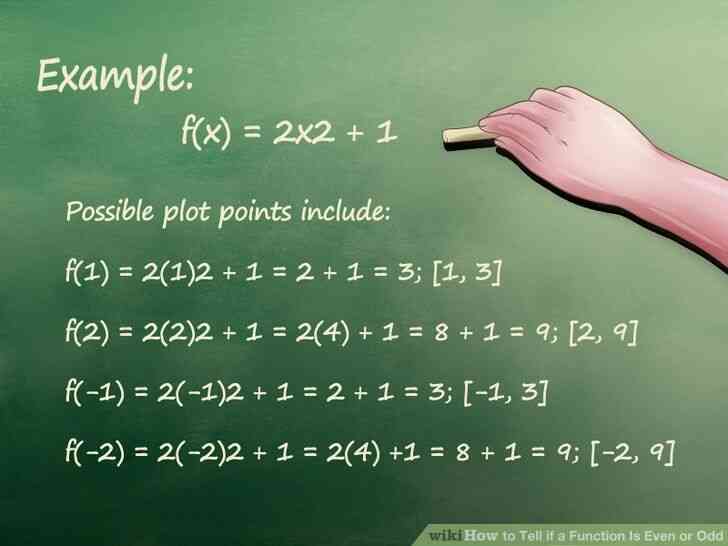
1
@@_
@@Tracer la fonction sur un graphique. Sortir un morceau de papier millimétré ou rapidement esquisser un blanc graphique avec l'axe des x et l'axe. Graphique de la fonction en branchant les différentes valeurs de x et de comprendre les résultats correspondants pour y créer des paires de coordonnées.
- Remarque que f(x) est le même que y lorsque le graphique d'une fonction.
- Numéro de l'axe des x et l'axe y.
- Pour tout x positif valeur de test, vous devez également tester le négatif correspondant x valeur.
- Exemple: f(x) = 2x2 1
- Possible de tracer les points suivants:
- f(1) = 2(1)2 1 = 2 1 = 3 [1, 3]
- f(2) = 2(2)2 1 = 2(4) 1 = 8 1 = 9 [2, 9]
- f(-1) = 2(-1)2 1 = 2 1 = 3 [-1, 3]
- f(-2) = 2(-2)2 1 = 2(4) 1 = 8 1 = 9 [-2, 9]
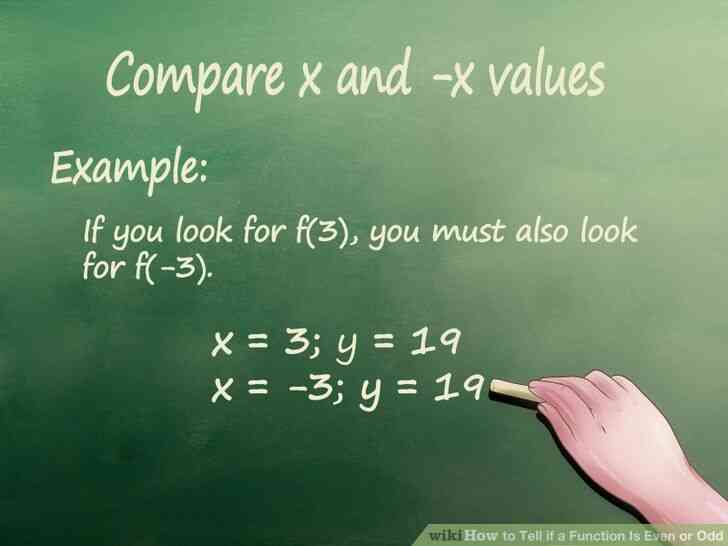
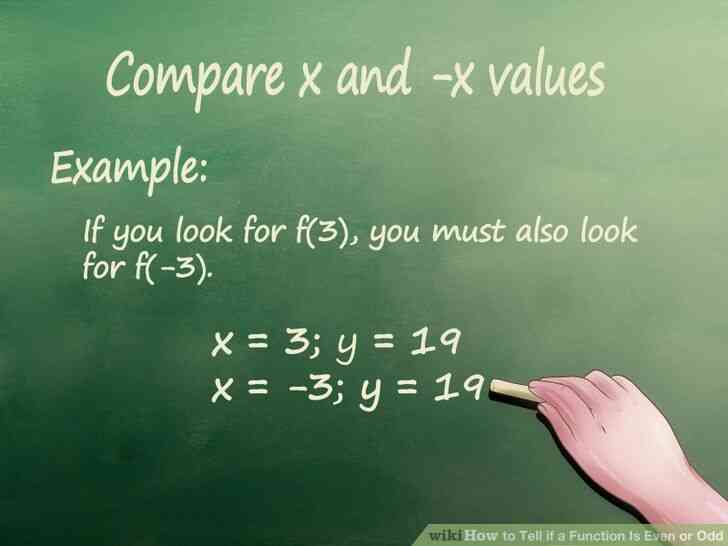
2
@@_
@@Comparer x et -x valeurs. Regardez votre graphique et de localiser les différentes valeurs de x pour la fonction. Pour chaque valeur de x, vous devez localiser la position de son correspondant -x valeur de point.
- Exemple: Si vous recherchez f(3), vous devez également rechercher de f(-3).
- x = 3 y = 19
- x = -3 y = 19


3
@@_
@@Analyser les résultats. Si la fonction est la même, il sera symétrique autour de l'axe y. Si la fonction est impaire, il va être symétriques par rapport à l'origine. Si elle n'est pas vraie, la fonction est ni le même ni impair.[3]
- 'Symétrique autour de l'axe y' signifie que le comportement de la courbe sur le côté gauche de l'axe des y reflète parfaitement ou reflète le comportement de la courbe sur le côté droit de l'axe des y.
- 'Symétriques par rapport à l'origine' signifie que le comportement de la courbe sur la partie inférieure gauche de l'ensemble du graphique reflète parfaitement le comportement de la fonction dans la partie supérieure droite de l'ensemble du graphique. De même, l'angle supérieur gauche et inférieur droit des parties du graphe sont des réflexions sont l'un de l'autre.
- Exemple: Pour chaque x de ce graphique, la valeur de y est la même que celle de son correspondant -x au point. En tant que telle, cette fonction est la même.
Supplémentaires Graphique Exemples de Méthode
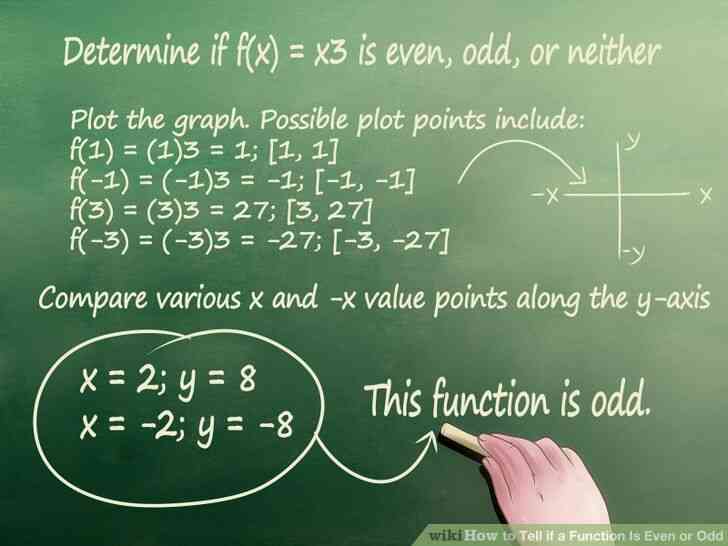
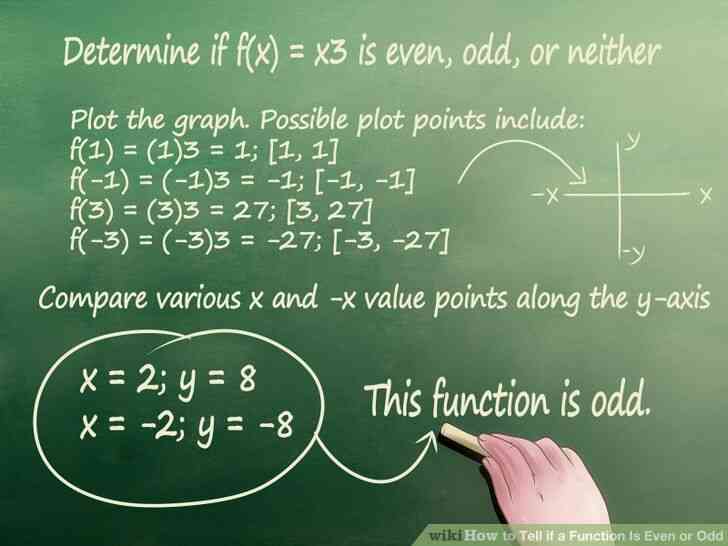
1
@@_
@@Déterminer si f(x) = x3 est pair, impair, ou autre.
- le graphe. Possible de tracer les points suivants:
- f(1) = (1)3 = 1 [1, 1]
- f(-1) = (-1)3 = -1 [-1, -1]
- f(3) = (3)3 = 27 [3, 27]
- f(-3) = (-3)3 = -27 [-3, -27]
- Comparer les différents x et -x de la valeur des points le long de l'axe en regardant des points de coordonnées. Match positives et négatives correspondantes valeurs de x.
- Déterminer si la fonction est paire ou impaire sur la base des résultats. Cette fonction est impaire.
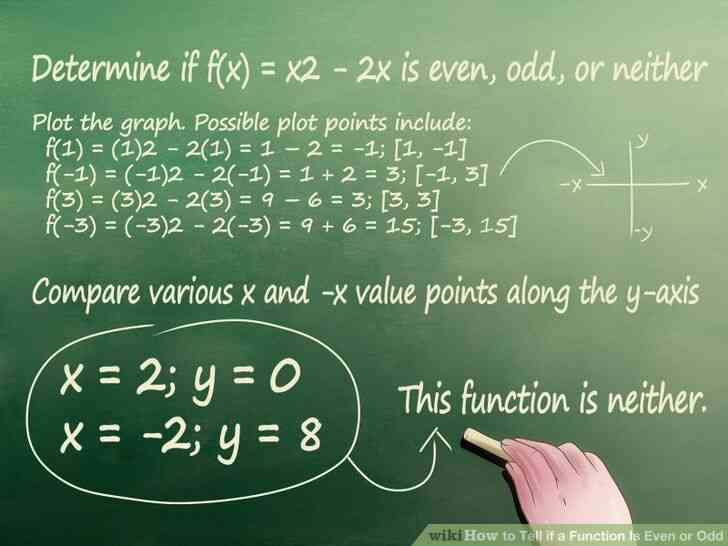
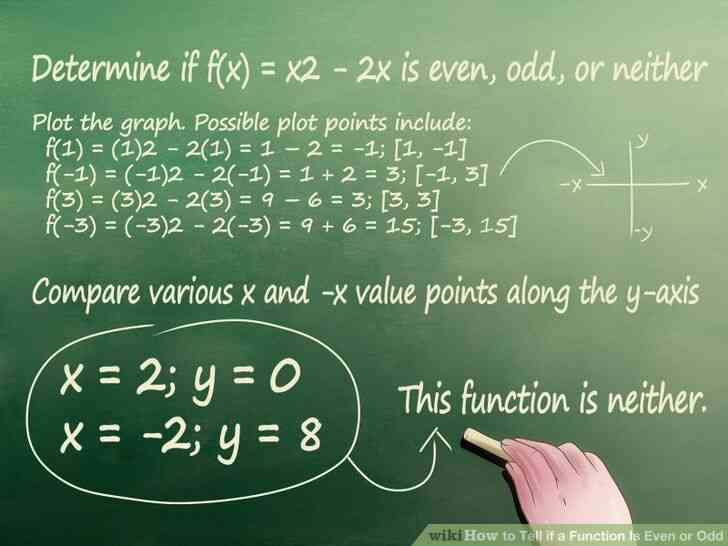
2
@@_
@@Déterminer si f(x) = x2 - 2x est pair, impair, ou autre.
- le graphe. Possible de tracer les points suivants:
- f(1) = (1)2 - 2(1) = 1 – 2 = -1 [1, -1]
- f(-1) = (-1)2 - 2(-1) = 1 2 = 3 [-1, 3]
- f(3) = (3)2 - 2(3) = 9 – 6 = 3 [3, 3]
- f(-3) = (-3)2 - 2(-3) = 9 6 = 15 [-3, 15]
- Comparer les différents x et -x de la valeur des points le long de l'axe en regardant des points de coordonnées. Match positives et négatives correspondantes valeurs de x.
- Déterminer si la fonction est paire ou impaire sur la base des résultats. Cette fonction est ni.
Comment savoir si une Fonction Est paire ou Impaire
Vous pouvez determiner si une fonction est pair, impair, ou ni en regardant l'equation elle-meme ou en regardant un graphique de cette fonction. A la fois la methode algebrique et le graphique de la methode sont assez simple, mais c'est une bonne idee de les mettre en pratique a la fois, de sorte que vous pouvez repondre a la question quel que soit le type d'information que vous avez sur la main.
Mesures
@@_
@@
Methode 1
a l'Aide de l'Algebre
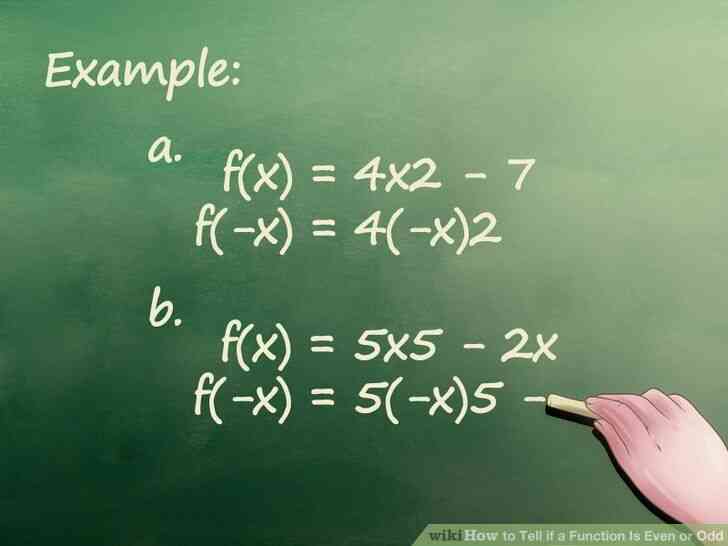
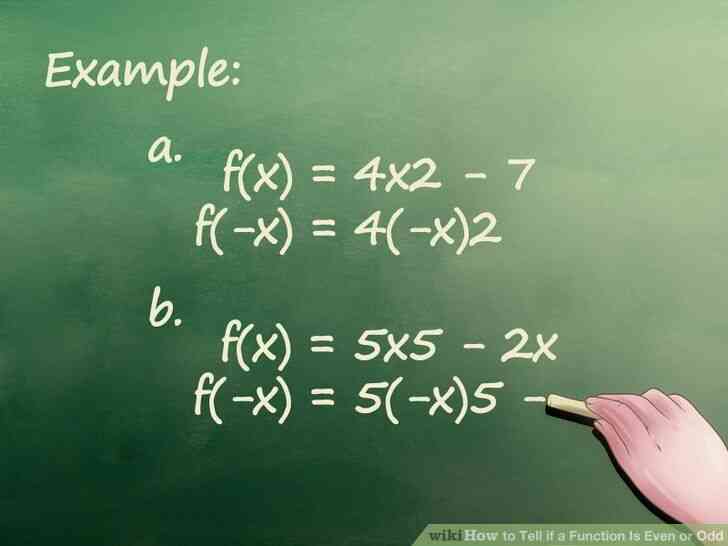
1
@@_
@@Plug-x dans la fonction d'origine. Regardez la fonction d'origine et de localiser la variable x. Chaque fois que vous voyez un x dans la fonction, remplacer-x.[1]
- Un Exemple: f(x) = 4x2 - 7
- dans l'Exemple B: f(x) = 5x5 - 2x
- Exemple C: f(x) = 7x2 5x 3
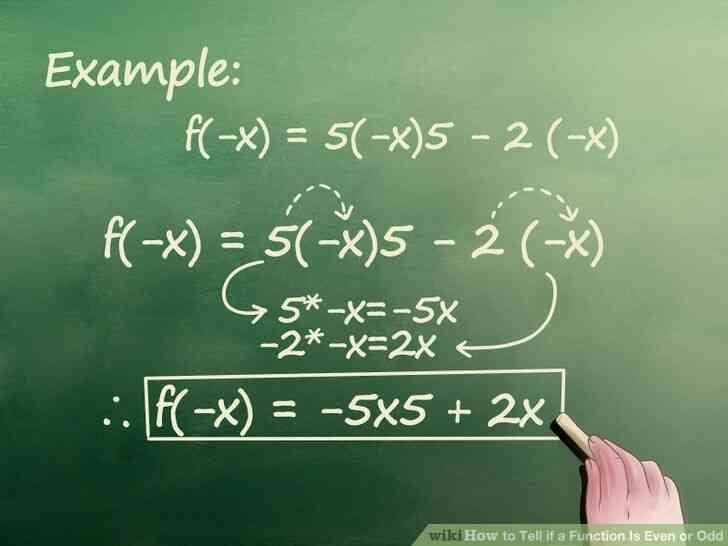
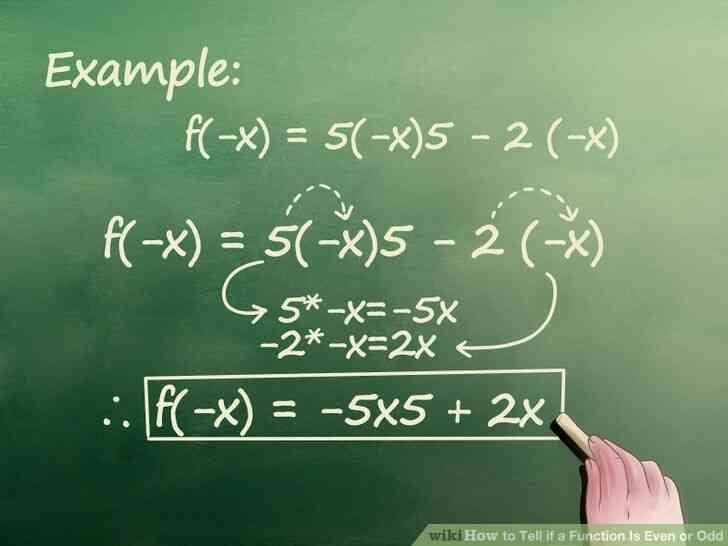
2
@@_
@@Resoudre l'equation. Evaluer l'equation en appliquant vos connaissances des exposants et la multiplication de se debarrasser de l'inutile, les signes negatifs.
- Un Exemple: f(-x) = 4(-x)2 - 7
- Un exposant negatif multiplie par lui-meme un meme nombre de fois va avoir un effet positif. C'est le principe mathematique que deux negatifs de l'egalite positive en termes de multiplication.
- f(-x) = 4(x)2 - 7
- dans l'Exemple B: f(-x) = 5(-x)5 - 2 (-x)
- Un exposant negatif multiplie par lui-meme un nombre impair de fois donne un resultat negatif. En outre, un signe negatif devant un exposant devra etre multipliee par le signe plus ou moins, qui se presente devant elle, et un signe negatif multiplie par un signe de la soustraction resultat sera un signe plus.
- f(-x) = -5 x 5 2x
- Exemple C: f(-x) = 7(-x)2 5(-x) 3
- Encore une fois, regardez les exposants, ainsi que les signes plus et moins. Meme les exposants auront pour resultat une valeur positive de x et de l'impair exposants un resultat negatif, x. Un signe negatif multiplie par un signe plus permettra de transformer le plus dans un signe moins, et vice-versa.
- f(-x) = 7x2 - 5x 3


3
@@_
@@Analyser les resultats. Si votre fonction est la meme que celle de votre depart de la fonction, la fonction est la meme. Si le resultat est a l'oppose ou negative de votre depart de la fonction, la fonction est impaire. Si elle n'est pas vraie, la fonction est ni le meme ni impair.[2]
- Dans une meme fonction, a la fois le debut et la fin des fonctions doit etre exactement le meme.
- Dans une fonction bizarre, tous les signes plus ( + ) doit devenir un signe moins et tous les signes moins doivent devenir des signes plus.
- Lorsqu'il est ecrit en symboles algebriques:
- Pour une meme fonction: f(x) = f(-x)
- Pour une fonction bizarre: f(-x) = -f(x)
- ni: f(-x) ? f(x) f(-x) ? -f(x)
- Un Exemple: f(x) = 4x2 - 7
- f(-x) = 4(x)2 - 7
- Cette fonction est la meme.
- Remarque, egalement, que chaque x dans une meme fonction ont generalement un exposant positif.
- dans l'Exemple B: f(x) = 5 x 5 - 2x
- f(-x) = -5 x 5 2x
- Cette fonction est impaire.
- de maniere generale, chaque partie de la fonction aura besoin d'etre accompagne par un x avec un etrange exposant de la fonction elle-meme etrange.
- Exemple C: f(x) = 7x2 5x 3
- f(-x) = 7x2 - 5x 3
- Cette fonction est ni le meme ni impair.
- Lorsque pairs et impairs, les exposants sont melanges a l'interieur d'une fonction, cette fonction sera probablement ni meme ni impair.
@@_
@@
Methode 2
a l'Aide de Graphiques
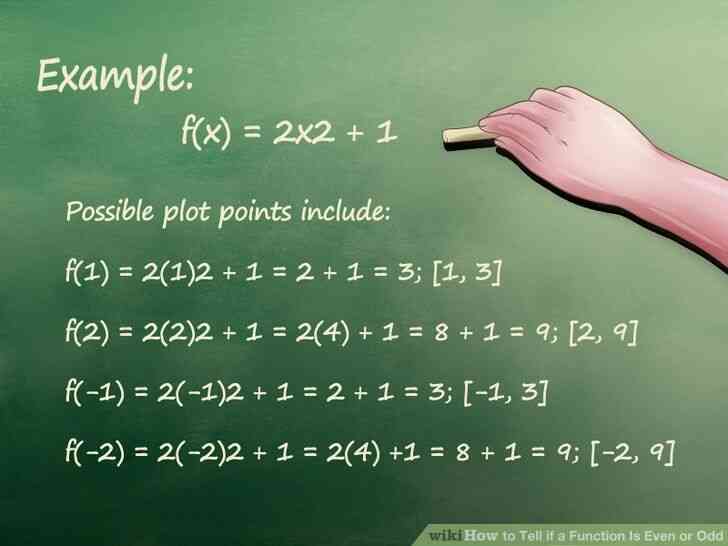
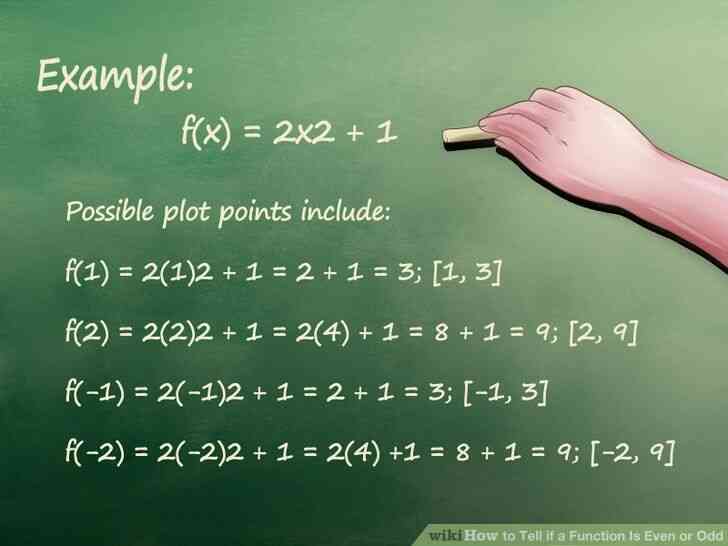
1
@@_
@@Tracer la fonction sur un graphique. Sortir un morceau de papier millimetre ou rapidement esquisser un blanc graphique avec l'axe des x et l'axe. Graphique de la fonction en branchant les differentes valeurs de x et de comprendre les resultats correspondants pour y creer des paires de coordonnees.
- Remarque que f(x) est le meme que y lorsque le graphique d'une fonction.
- Numero de l'axe des x et l'axe y.
- Pour tout x positif valeur de test, vous devez egalement tester le negatif correspondant x valeur.
- Exemple: f(x) = 2x2 1
- Possible de tracer les points suivants:
- f(1) = 2(1)2 1 = 2 1 = 3 [1, 3]
- f(2) = 2(2)2 1 = 2(4) 1 = 8 1 = 9 [2, 9]
- f(-1) = 2(-1)2 1 = 2 1 = 3 [-1, 3]
- f(-2) = 2(-2)2 1 = 2(4) 1 = 8 1 = 9 [-2, 9]
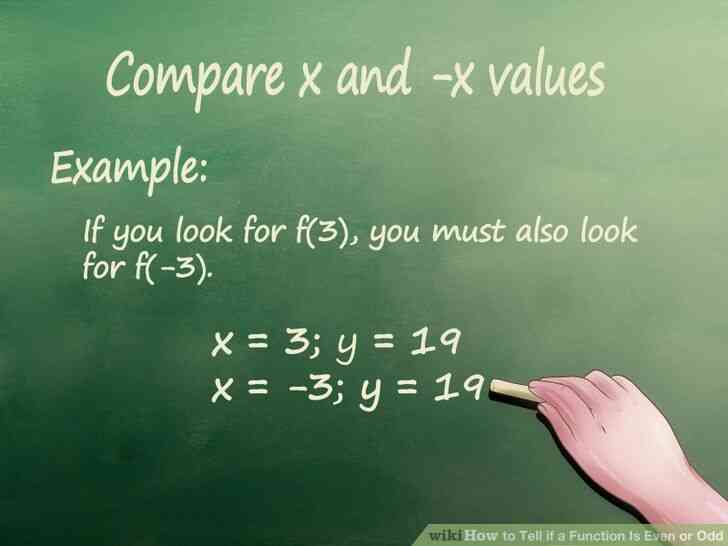
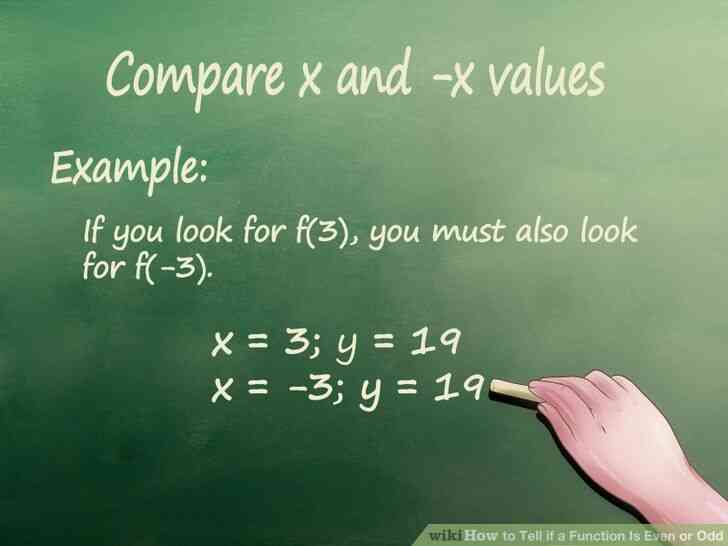
2
@@_
@@Comparer x et -x valeurs. Regardez votre graphique et de localiser les differentes valeurs de x pour la fonction. Pour chaque valeur de x, vous devez localiser la position de son correspondant -x valeur de point.
- Exemple: Si vous recherchez f(3), vous devez egalement rechercher de f(-3).
- x = 3 y = 19
- x = -3 y = 19


3
@@_
@@Analyser les resultats. Si la fonction est la meme, il sera symetrique autour de l'axe y. Si la fonction est impaire, il va etre symetriques par rapport a l'origine. Si elle n'est pas vraie, la fonction est ni le meme ni impair.[3]
- 'Symetrique autour de l'axe y' signifie que le comportement de la courbe sur le cote gauche de l'axe des y reflete parfaitement ou reflete le comportement de la courbe sur le cote droit de l'axe des y.
- 'Symetriques par rapport a l'origine' signifie que le comportement de la courbe sur la partie inferieure gauche de l'ensemble du graphique reflete parfaitement le comportement de la fonction dans la partie superieure droite de l'ensemble du graphique. De meme, l'angle superieur gauche et inferieur droit des parties du graphe sont des reflexions sont l'un de l'autre.
- Exemple: Pour chaque x de ce graphique, la valeur de y est la meme que celle de son correspondant -x au point. En tant que telle, cette fonction est la meme.
Supplementaires Graphique Exemples de Methode
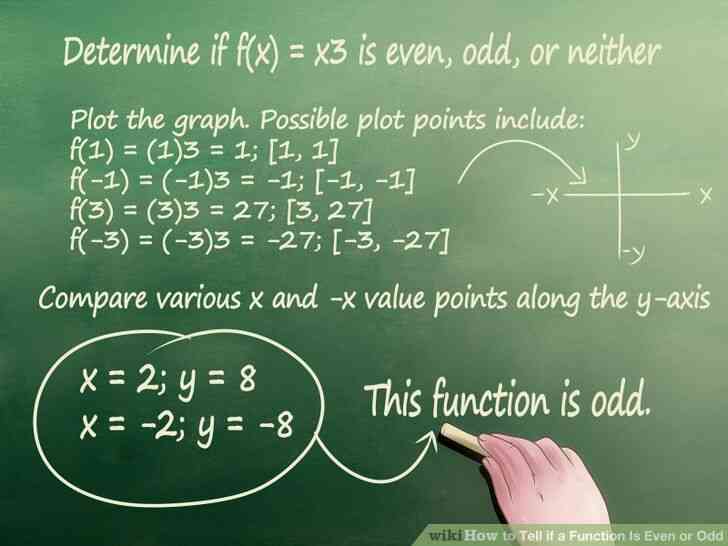
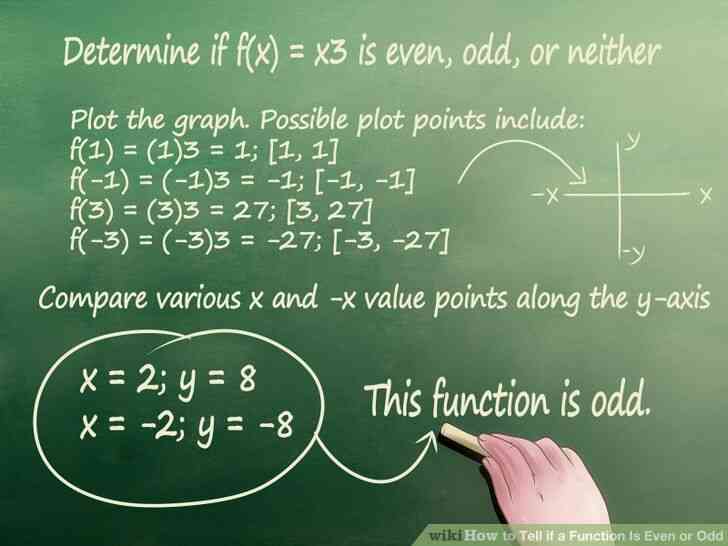
1
@@_
@@Determiner si f(x) = x3 est pair, impair, ou autre.
- le graphe. Possible de tracer les points suivants:
- f(1) = (1)3 = 1 [1, 1]
- f(-1) = (-1)3 = -1 [-1, -1]
- f(3) = (3)3 = 27 [3, 27]
- f(-3) = (-3)3 = -27 [-3, -27]
- Comparer les differents x et -x de la valeur des points le long de l'axe en regardant des points de coordonnees. Match positives et negatives correspondantes valeurs de x.
- Determiner si la fonction est paire ou impaire sur la base des resultats. Cette fonction est impaire.
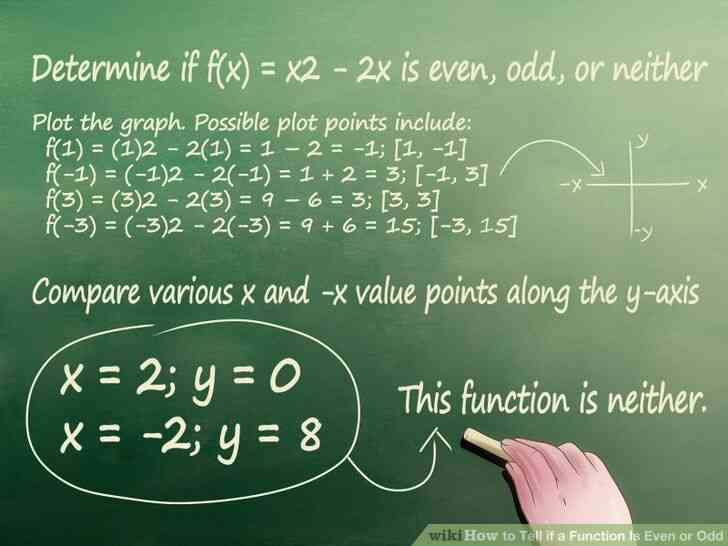
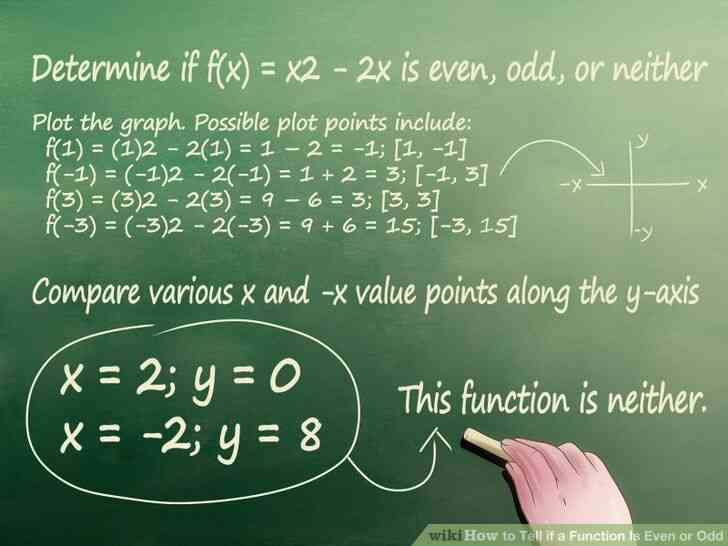
2
@@_
@@Determiner si f(x) = x2 - 2x est pair, impair, ou autre.
- le graphe. Possible de tracer les points suivants:
- f(1) = (1)2 - 2(1) = 1 – 2 = -1 [1, -1]
- f(-1) = (-1)2 - 2(-1) = 1 2 = 3 [-1, 3]
- f(3) = (3)2 - 2(3) = 9 – 6 = 3 [3, 3]
- f(-3) = (-3)2 - 2(-3) = 9 6 = 15 [-3, 15]
- Comparer les differents x et -x de la valeur des points le long de l'axe en regardant des points de coordonnees. Match positives et negatives correspondantes valeurs de x.
- Determiner si la fonction est paire ou impaire sur la base des resultats. Cette fonction est ni.
Comment savoir si une Fonction Est paire ou Impaire
By commentfaire
Vous pouvez déterminer si une fonction est pair, impair, ou ni en regardant l'équation elle-même ou en regardant un graphique de cette fonction. À la fois la méthode algébrique et le graphique de la méthode sont assez simple, mais c'est une bonne idée de les mettre en pratique à la fois, de sorte que vous pouvez répondre à la question quel que soit le type d'information que vous avez sur la main.