Peut-être vous êtes un artiste ou un designer d'intérieur ou architecte, ou peut-être vous êtes dans la géométrie en tant que discipline de la logique. Ici est la façon de déterminer un cercle et le carré de l'égalité des zones, et plus loin, de comprendre le sens de la racine carrée de pi. Utiliser r1 à l'égalité du côté d'un carré et r2 représentent le rayon du cercle correspondant.
Mesures
@@_
@@
Partie 1
Le tuto


1
@@_
@@Laissez r1^2) représente la zone de la place, Un(s).


2
@@_
@@Laissez pr2^2 = l'aire du cercle, Un(c).
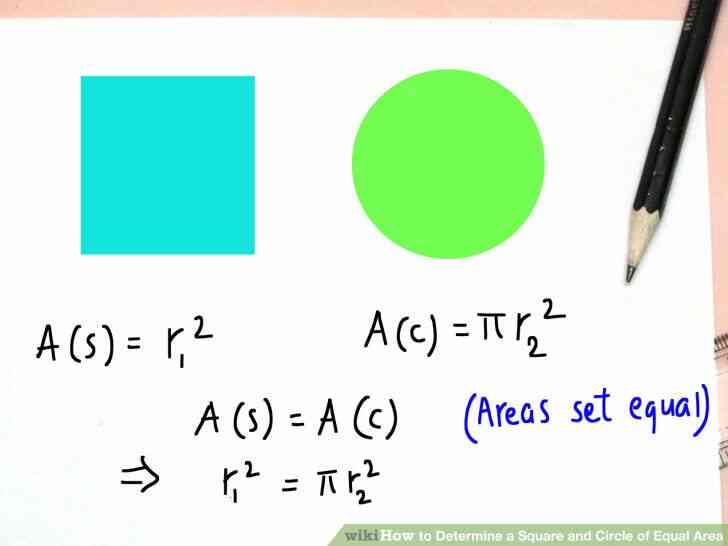
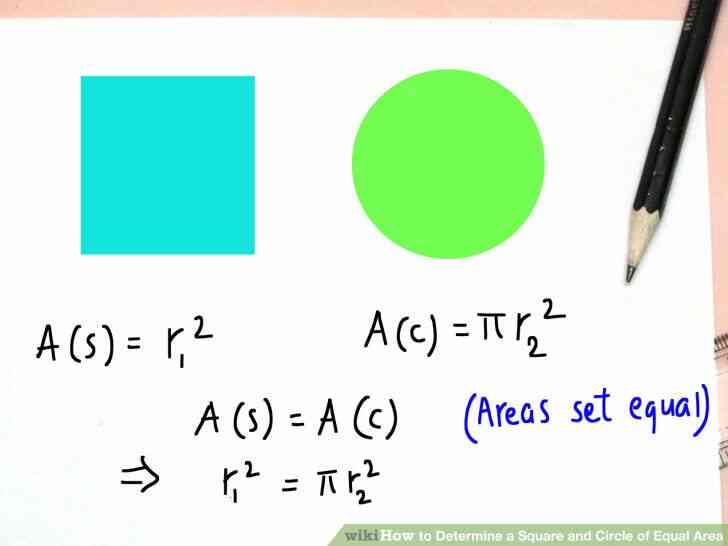
3
@@_
@@de la série A(s) = A(c) par r1^2 = pr2^2.


4
@@_
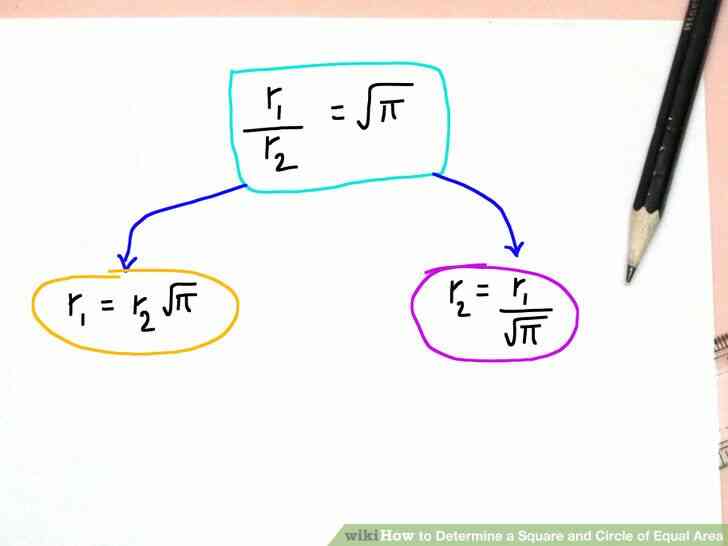
@@Puis r1^2 / r2^2 = p et r1 / r2 = sqrt(p).

5
@@_
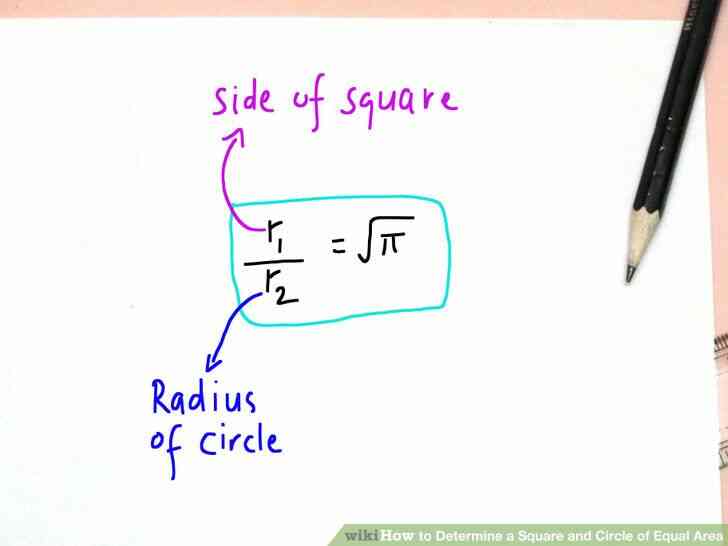
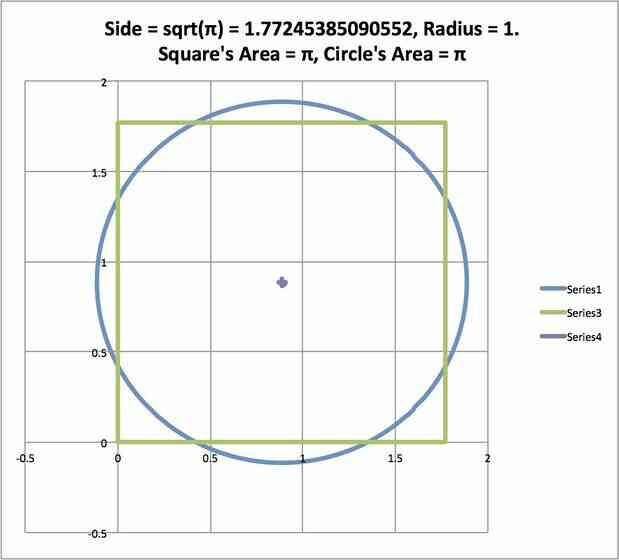
@@Donné soit r1 ou r2, nous pouvons déterminer à l'autre. Qui est: r1 = sqrt(p)*r2 et r2 = r1/sqrt(p). sqrt(p) = 1.77245385090552. Donc, étant donné un carré de côté r1 = 1.77245385090552, sa superficie = 1.77245385090552^2 = p et r2 = r1/sqrt(p) ou 1.77245385090552/1.77245385090552 = 1 et la zone de r2 du cercle = pr2^2 = p(1)^2 = p, ce qui est égal à la surface de la place vient d'être calculée.

6
@@_
@@Et il a été appris que la racine carrée de p la relation entre l'égalité des zones d'un cercle et le carré de la variable 'rayon de.'@@_
@@
Partie 2
Explicatives des Tableaux, des Diagrammes, des Photos

1
@@_
@@@@_
@@
Partie 3
Conseils
1
@@_
@@Rendre l'utilisation de l'aide en fonction des articles au moment de passer au travers de ce tutoriel:


2
@@_
@@
Comment Determiner un Cercle et le Carre de meme Aire
Peut-etre vous etes un artiste ou un designer d'interieur ou architecte, ou peut-etre vous etes dans la geometrie en tant que discipline de la logique. Ici est la façon de determiner un cercle et le carre de l'egalite des zones, et plus loin, de comprendre le sens de la racine carree de pi. Utiliser r1 a l'egalite du cote d'un carre et r2 representent le rayon du cercle correspondant.
Mesures
@@_
@@
Partie 1
Le tuto


1
@@_
@@Laissez r1^2) represente la zone de la place, Un(s).


2
@@_
@@Laissez pr2^2 = l'aire du cercle, Un(c).
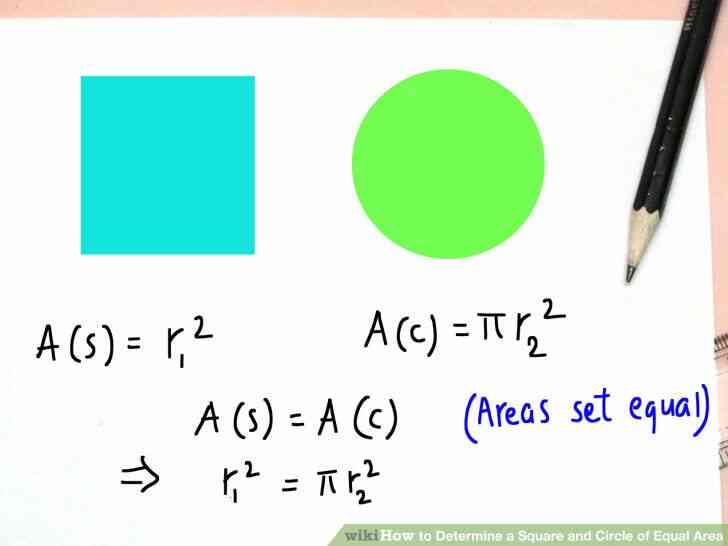
3
@@_
@@de la serie A(s) = A(c) par r1^2 = pr2^2.


4
@@_
@@Puis r1^2 / r2^2 = p et r1 / r2 = sqrt(p).


5
@@_
@@Donne soit r1 ou r2, nous pouvons determiner a l'autre. Qui est: r1 = sqrt(p)*r2 et r2 = r1/sqrt(p). sqrt(p) = 1.77245385090552. Donc, etant donne un carre de cote r1 = 1.77245385090552, sa superficie = 1.77245385090552^2 = p et r2 = r1/sqrt(p) ou 1.77245385090552/1.77245385090552 = 1 et la zone de r2 du cercle = pr2^2 = p(1)^2 = p, ce qui est egal a la surface de la place vient d'etre calculee.


6
@@_
@@Et il a ete appris que la racine carree de p la relation entre l'egalite des zones d'un cercle et le carre de la variable 'rayon de.'@@_
@@
Partie 2
Explicatives des Tableaux, des Diagrammes, des Photos


1
@@_
@@@@_
@@
Partie 3
Conseils
1
@@_
@@Rendre l'utilisation de l'aide en fonction des articles au moment de passer au travers de ce tutoriel:


2
@@_
@@
Comment Déterminer un Cercle et le Carré de même Aire
By commentfaire
Peut-être vous êtes un artiste ou un designer d'intérieur ou architecte, ou peut-être vous êtes dans la géométrie en tant que discipline de la logique. Ici est la façon de déterminer un cercle et le carré de l'égalité des zones, et plus loin, de comprendre le sens de la racine carrée de pi. Utiliser r1 à l'égalité du côté d'un carré et r2 représentent le rayon du cercle correspondant.